Quantum Simulations with long strings of Trapped Ions
We have open positions for PhD students and Postdocs!
In our experiments, we simulate and investigate quantum phenomena with up to 51, individually controllable qubits, represented by trapped calcium ions. Our focus lies on quantum state estimation, entanglement characterization, and time-evolution of many-body systems. Furthermore, we work with a novel approach to quantum simulation, where complex quantum states are prepared variationally, using a feedback loop between a classical computer and our quantum computer.
Simultaneously we are always working on the development of our experimental setup. For example, we improve the experiment control software, automize experimental sequences, develop electronic circuits, program efficient analysis tools, and design an optical setup to allow for the full control of up to 51 qubits.

Our laboratory. Photo: IQOQI / M. R. Knabl
On Quantum simulation
The discovery of quantum theory has provided us with an immensely successful tool for explaining complex phenomena in many areas of natural sciences. The field of “Quantum Simulation” was introduced in the 1980's when Richard Feynman and others proposed a new method for approaching quantum mechanical problems that are too hard to solve on ordinary computers. The idea is to mimic (simulate) complex quantum effects of interest by using a more accessible quantum system as the computing device.
Trapped ions allow us to reliably prepare a quantum state, control its dynamical evolution, create entanglement and carry out quantum measurements. This excellent control over all these quantum degrees of freedom makes trapped ions very suitable for realising quantum simulators and to study quantum physics at the most fundamental level.
Our experimental platform
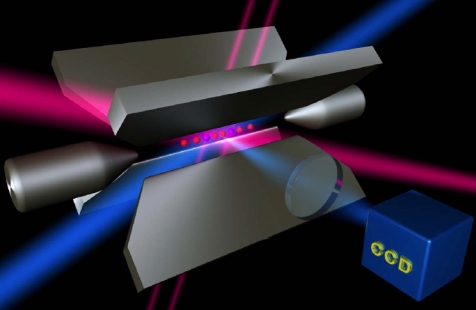
We work with linear strings of trapped calcium ions that are stored for hours by a combination of radio-frequency fields and electrostatic potentials (linear Paul trap). Using ultrastable lasers, we cool the ion motion to the ground state of the potential provided by the ion trap and prepare the ions in particular quantum states. In detail, we can encode a quantum bit of information in two long-lived electronic states. The absorption of a photon by an ion is accompanied by momentum transfer. Therefore, it is possible to control the quantized motion of the ions using laser light and to entangle the ion motion with the ions’ internal electronic states. Moreover, this kind of coupling can be used to create entanglement between the internal states of many ions. The capability to address individual qubits with a tightly focused laser beam rounds our set of quantum gates.
|
|
Linear Paul trap | Sketch of the experimental setup |
Latest publications
- Characterization of ion-trap-induced ac magnetic fields, Phys. Rev. A 110, 63101 (2024)
- Observing the quantum Mpemba effect in quantum simulations, PRL 133, 10402 (2024)
- Exploring Large-Scale Entanglement in Quantum Simulation, Nature 624, 539 (2023)
- Quantum-enhanced sensing on optical transitions through finite-range interactions, Nature 621, 740 (2023)
- Observation of magnon bound states in the long-range, anisotropic Heisenberg model, Phys. Rev. X 13, 031017-12 (2023)
- Experimental observation of thermalization with noncommuting charges, PRX Quantum 4, 20318 (2023)
- Observing emergent hydrodynamics in a long-range quantum magnet, Science 376, 720 (2022)
- Controlling long ion strings for quantum simulation and precision measurements, Phys. Rev. A 105, 52426 (2022)
Project Members
- Marco Lucibello (PhD student)
- Giorgio Ciocca (Master student)
- Johannes Franke (PhD student)
- Manoj K. Joshi (Postdoc)
- Florian Kranzl (PhD student)
- Ben Lanyon (Senior scientist)
- Christian Roos (Project leader)
- Rainer Blatt (Group leader)
Former members: Tiffany Brydges, Christine Maier, Lukas Pernthaler, Petar Jurcevic, Christoph Steinlechner, Heng Shen, Cornelius Hempel, Sebastian Schunke, Florian Zähringer, Markus Rambach, René Gerritsma, Gerhard Kirchmair, Jan Benhelm, Timo Körber, Umakant Rapol.
Further Reading
PhD theses of Jan Benhelm, Gerhard Kirchmair, Florian Zähringer, Cornelius Hempel and Petar Jurcevic