Quantum simulation of the Klein paradox

In an experiment carried out in 2009, our group has performed a quantum simulation of the Dirac equation using a single trapped ion [1] and observed so called Zitterbewegung, a peculiar quivering motion of free relativistic quantum particles predicted by the Dirac equation. In a recent experiment we have implemented a more sophisticated quantum simulation, which made it possible to observe another counter-intuitive prediction of the Dirac equation: the Klein paradox [2].

Quantum simulation

In the 1980s Richard Feynman and others proposed a new method to tackle quantum mechanical problems that are too hard to solve on ordinary computers. Their idea was to simulate them using another quantum system that can be accurately controlled in a laboratory. To date, only a few quantum systems can be controlled well enough to begin exploring their use as quantum simulators [4]. Cold trapped ions (charged atoms) are a leading candidate, as their quantum state can be manipulated and measured with high fidelity. In recent years the first quantum simulations have been performed using trapped ions. Although these experiments show how quantum simulation would work in principle, they have not yet reached a level of sophistication such that they can compete with normal computers. It is expected that this will only happen once the simulation has to be performed for a larger number of quantum particles, which in the case of trapped ions means a larger number of ions and possibly lasers performing the simulation. Currently, this is still out of technological reach, as only about ten ions can be stored and manipulated at a time, while outperforming a classical computer would require ~40 ions. On the other hand, small scale quantum simulation can reveal interesting similarities in physics describing seemingly unrelated systems. In our quantum simulator for instance, trapped ions that are very cold (less than 0.001 K) can be made to behave like particles having a speed close to the speed of light, such that their dynamics is described by relativistic quantum mechanics: The Dirac equation.

The Klein paradox

The Dirac equation was put forward in 1928 to describe a relativistic quantum particle. Interestingly, the Dirac equation had to incorporate 'spin', a new degree of freedom for particles found some time before, to make sense. It also successfully predicted the existence of anti-matter and it is used to make extraordinary precise predictions on for instance the spectrum of the Hydrogen atom that are confirmed by experiment. The Dirac equation also predicted a number of counter-intuitive effects, of which Zitterbewegung (a quivering motion of a free Dirac particle) and the Klein paradox are the best known. The Klein paradox was first described by Oskar Klein in 1928 when investigating scattering of relativistic particles described by the Dirac equation. Klein found that a relativistic particle encountering a potential step larger than its kinetic energy has a probability to be transmitted, whereas intuition would have this particle reflect completely, as is the case for non-relativistic particles. The paradox was later resolved in quantum field theory by the notion of particle/anti particle creation at the barrier. While the paradox is a much debated topic, which in part is due to its emergence in graphene [5], direct investigations of the phenomena have yet to be realised due to the immense experimental difficulties involved (enormous electric field gradients are required, for example).

The Klein paradox in trapped ions

A few years ago, Enrique Solano, a theoretical physicist now working in Spain, and his co-workers discovered that the equations describing the dynamics of the trapped ion coupled to certain laser fields resemble the Dirac equation [6]. Working together with him our group performed a quantum simulation of the Dirac equation for a free relativistic particle, and observed Zitterbewegung in the motion of this particle [1]. To observe the Klein paradox however, required letting this particle smash against a potential barrier. Since the dynamics of the Dirac particle takes place on a length scale that is much smaller than the wavelength of the lasers at our disposal, it is not possible to engineer this potential barrier in a direct way. However, using a second trapped ion interacting with laser light we were able to let the simulated Dirac particle collide with a linear potential (a slope) [3]. It was shown already in 1931 by Fritz Sauter that the Klein paradox should also occur for such a potential, and he calculated the expected probability for tunneling.

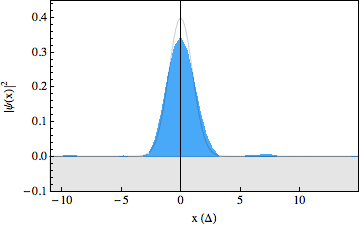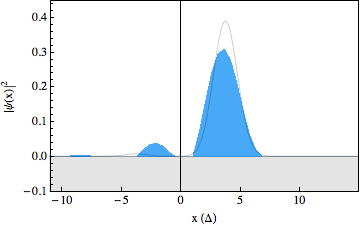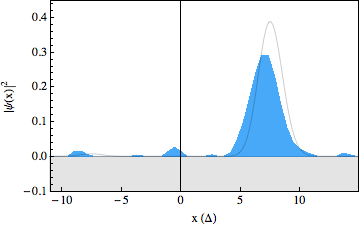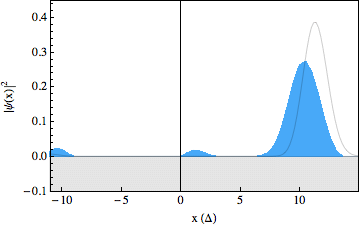
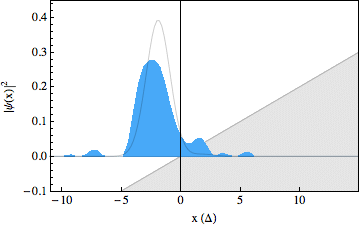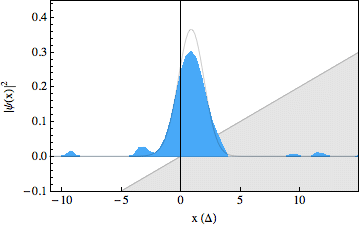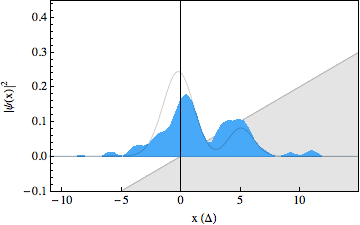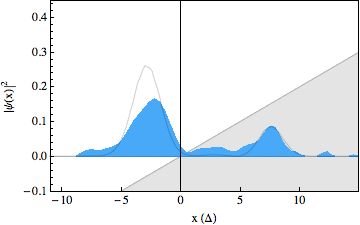
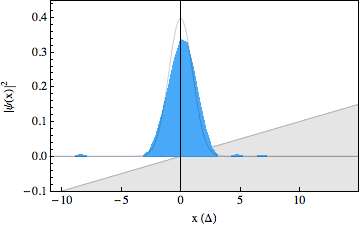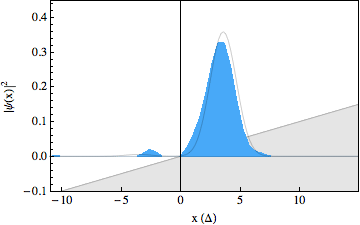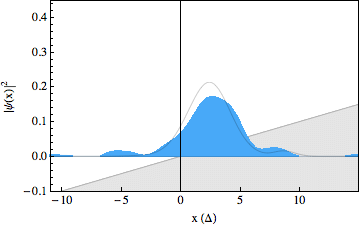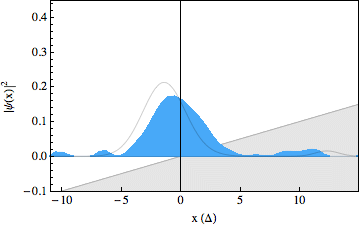In the experiment, we were able to use recently developed techniques to make snapshots of the particles wavepacket during the scattering process, resulting in a movie showing the occurrence of the Klein paradox (see figures below). The first movie shows a free Dirac particle that moves in a straight line, as expected. Note that there is no Zitterbewegung for this particle, as it is made up completely out of positive energy components. In the second movie we switched on a gentle slope, on which the particle reflects. In the third movie we increased the strength of this slope and we can see that part of the wavepacket tunnels through as predicted by the Klein paradox. The solid lines in the movies show what we would expect to happen from theory. Note that the spinor components for these wavepackets have been traced out.

What's next

The present quantum simulation is by no means a quantum simulation of the kind that cannot be done on a classical computer. To make the quantum simulation less computable by classical computers it needs to be more complicated, for instance by adding more particles. Another interesting direction might be the study of quantum fields. We are currently also looking into the quantum simulation of another relativistic wave equation, the Majorana equation. This model may underly the nature of neutrinos or exotic theories outside the standard model [7]. The quantum simulation of this equation would be very curious, as it has a very peculiar mathematical form which is not given by a Hamiltonian. In fact it describes the dynamics of particles in a way that is completely different than (relativistic) quantum mechanics and has never been observed in nature. Still, our quantum computer, firmly described by quantum mechanics, can be used to simulate such dynamics, much in the same way as a desktop computer can be used to simulate any system.

See also: Physics synopsis

Literature

[1] Quantum simulation of the Dirac equation. R. Gerritsma, G. Kirchmair, F. Zähringer, E. Solano, R. Blatt and C.F. Roos, Nature 463, 68 (2010) pdf

[2] Quantum simulation of the Klein paradox with trapped ions R. Gerritsma, B.P. Lanyon, G. Kirchmair, Zähringer, C. Hempel, J. Casanova, J.J. Garcia-Ripoll, E. Solano, R. Blatt and C.F. Roos, Phys. Rev. Lett. 106, 060503 (2011) pdf

[3] Klein tunneling and Dirac potentials in trapped ions J. Casanova, J. J. Garcia-Ripoll, R. Gerritsma, C. F. Roos, E. Solano, Phys. Rev. A 82, 020101(R) (2010) pdf

[4] Quantum simulators, I. Buluta and F. Nori, Science 326, 108 (2009) pdf

[5] Quantum interference and Klein tunnelling in graphene heterojunctions, A.F. Young and P. Kim, Nature Physics 5, 222 (2009) pdf

[6] Dirac equation and quantum relativistic effects in a single trapped ion, L. Lamata, J. Léon, T. Schätz and E. Solano, Phys. Rev. Lett. 98, 253005 (2007) pdf

[7] Quantum Simulation of the Majorana Equation and Unphysical Operations, J. Casanova, C. Sabin, J. Leon, I. L. Egusquiza, R. Gerritsma, C. F. Roos, J. J. Garcia-Ripoll and E. Solano, Phys. Rev. X 1, 021018 (2011) pdf

Financial support

We are financially supported by Österreichische Akademie der Wissenschaften, Universität Innsbruck, Fonds zur Förderung der wissenschaftlichen Forschung (FWF) within the program "Foundations and Applications of Quantum Science", the European Union as well as IQI and IARPA.