Quantum simulation of the Dirac equation
In a recent experiment [1], our group has performed a quantum simulation of the Dirac equation using a single trapped ion and observed so called Zitterbewegung, a peculiar quivering motion of free relativistic quantum particles predicted by the Dirac equation.
Quantum mechanics and special relativity
Quantum mechanics was developed in the first half of the 20th century to describe the dynamics of small particles, such as atoms and electrons. By the mid 1920s physicists had established the equations governing the dynamics of these quantum particles in the non-relativistic limit (i.e. for particles with a small velocity compared to the speed of light). It was well known by then that a full description should incorporate Einstein's theory of special relativity, dating from 1905, to account for high particle velocities. The Dirac equation was put forward in 1928 to describe a relativistic quantum particle. Interestingly, the Dirac equation had to incorporate 'spin', a new degree of freedom for particles found some time before, to make sense. Until that time, the spin had been added artificially to the equations. It came as a big surprise that the Dirac equation predicted even one more degree of freedom: anti-matter. This prediction was confirmed in 1933 with the discovery of the positron. Today, the Dirac equation is used to make extraordinary precise predictions on for instance the spectrum of the hydrogen atom that are confirmed by experiment and it is the starting point of more accurate theories known as quantum field theories.
Zitterbewegung
Despite these successes it was found shortly after the publication of Dirac's results that his equation also made a number of counterintuitive predictions. A well known example is a quivering motion ("Zitterbewegung") of a free particle first examined by Schrödinger [2]. This effect is peculiar because according to Newton's first law, a particle that experiences no forces should move in a straight line. In real quantum particles, such as electrons, the Zitterbewegung would have a very small amplitude (10-13 m) and an extremely high frequency (1021 Hz) and has never been observed. It has been debated whether this effect would survive in a more accurate quantum field theoretical description and whether it can be observed at all.
Quantum simulation
In the 1980s Feynman and others proposed a new method for approaching quantum mechanical problems that are too hard to solve on ordinary computers. Their idea was to simulate them using a more accessible quantum system in a laboratory. To date, only a few quantum systems can be controlled well enough to act as a quantum simulator and the simulations have not been very advanced but rather proof-of-principle experiments. Still, these first steps are very interesting for physicist because, as with the quantum simulation described here, the simulated system is experimentally very hard to access otherwise.
A trapped ion quantum simulator
In our group and others, single ions are routinely trapped and manipulated with laser light. A few years ago, Enrique Solano, a theoretical physicist now working in Spain, and his co-workers discovered that the equations describing the dynamics of the trapped ion coupled to certain laser fields resemble the Dirac equation [3]. Having established that the Dirac equation could be simulated in this way, it still remained a problem to measure the Zitterbewegung that might occur. Although the amplitude of the Zitterbewegung in the trapped ion is much larger than for a relativistic electron, it is still only a few nanometer, much too small to observe with the technology available in the lab. To solve this problem Solano and his team proposed a mapping that transferred the position of the ion onto the easily detectable internal state of the ion. In the following collaboration, this technique was further developed in our group. The figure below shows the average position of the simulated particle (i.e. the ion) for different (simulated) masses. The lightest of these particles (corresponding to the red line) has zero mass and it moves with the velocity of light (which is less than 1mm/s in this simulation). For higher masses the particle moves slower and no longer on a straight line: Zitterbewegung appears! Zitterbewegung measured in a single ion. The vertical axis represents the the average position of the ion measured in units of its minimum width (about 9 nm), the horizontal axis represents time. The curves are for different particle masses. For zero mass (the red points) there is no Zitterbewegung. As the mass increases the frequency of the Zitterbewegung goes up, but the amplitude goes down.
What's next
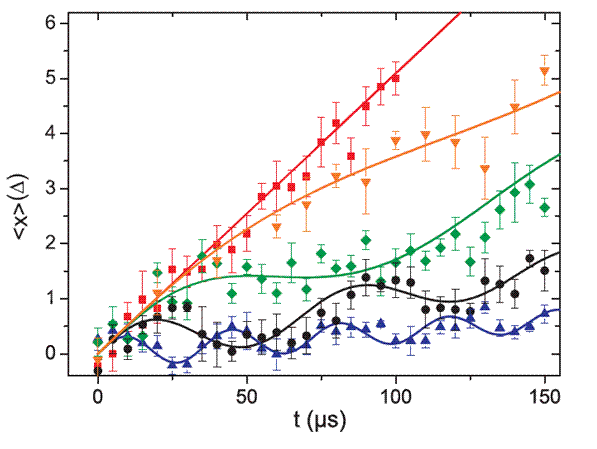The trapped ion system allows us investigate the dynamics of relativistic quantum systems for a wide range of parameters and initial conditions, still it is by no means a quantum simulation of the kind that cannot be done on a classical computer. The solid lines in the figure on the right were for instance computed on a classical computer in very short amount of time. To make the quantum simulation less computable by classical computers it needs to be more complicated, for instance by adding more particles, or quantum fields. Another improvement would be increasing the dimensionality, in the present experiment we simulated a Dirac particle living in just one dimension, significantly simplifying the required laser setup. On the other hand it will be interesting to simulate other peculiar relativistic dynamics, in particular the other counterintuitive effect predicted by the Dirac equation: The Klein paradox [4].
See also: Nature News & Views
Literature
[1] Quantum simulation of the Dirac equation. R. Gerritsma, G. Kirchmair, F. Zähringer, E. Solano, R. Blatt and C.F. Roos, Nature 463, 68 (2010) pdf
[2] Über die kräftfreie Bewegung in der relativistischen Quantenmechanik. E. Schrödinger, Sitz. Preuss. Akad. Wiss. Phys.-Math. Kl. 24, 418-428 (1930)
[3] Dirac equation and quantum relativistic effects in a single trapped ion, L. Lamata, J. Léon, T. Schätz and E. Solano, Phys. Rev. Lett. 98, 253005 (2007) pdf
[4] Die Reflexion von Elektronen an einem Potentialsprung nach der relativistischen Dynamic von Dirac , O. Klein Z. Phys. 53, 157-165 (1929)
Downloads
Financial support
We are financially supported by Österreichische Akademie der Wissenschaften, Universität Innsbruck, Fonds zur Förderung der wissenschaftlichen Forschung (FWF) within the program "Foundations and Applications of Quantum Science", the European network "SCALA" as well as IQI and IARPA.