Efficient tomography of a quantum many-body system

Efficient tomography of a quantum many-body system.
  B. P. Lanyon, C. Maier, M. Holzäpfel, T. Baumgratz, C. Hempel, P. Jurcevic, I. Dhand, A. S. Buyskikh, A. J. Daley, M. Cramer, M. B. Plenio, R. Blatt, C. F. Roos
Nature Physics 13, 1158 (2017)
arXiv version:pdf

Full quantum state tomography has become the standard experimental tool for the complete characterization of small quantum systems comprised of up to 8 quantum particles [1]. Since the measurement effort required grows exponentially with the number of qubits, this brute-force approach is unsuitable for characterizing quantum systems with more than ten qubits as are currently being developed in various experimental platforms. For this reason, new state characterization tools are required and are being developed for the study of many-body quantum systems [2-7].

To study the experimental implementation of a particularly promising strategy – matrix product state tomography – we started a collaboration between the Innsbruck ion trapping group and the controlled-quantum dynamics group led by M. Plenio at the University of Ulm and the quantum optics and quantum many-body systems group led by A. Daley at the University of Strathclyde.  

As a result of this collaboration, we  demonstrated the efficient characterization of a quantum many-body system of up to 14 entangled ions. Matrix product states (MPS) offer a compact description of a wide class of physically relevant quantum states in which strong quantum correlations exist locally. Matrix product state tomography [2] exploits this feature by building a representation of the quantum state of a system that is based on measuring local correlations between the state’s constituents. In our work, we apply MPS tomography to non-equilibrium states of a trapped-ion quantum simulator and experimentally demonstrate key features, limitations, extensions and new applications of this approach.

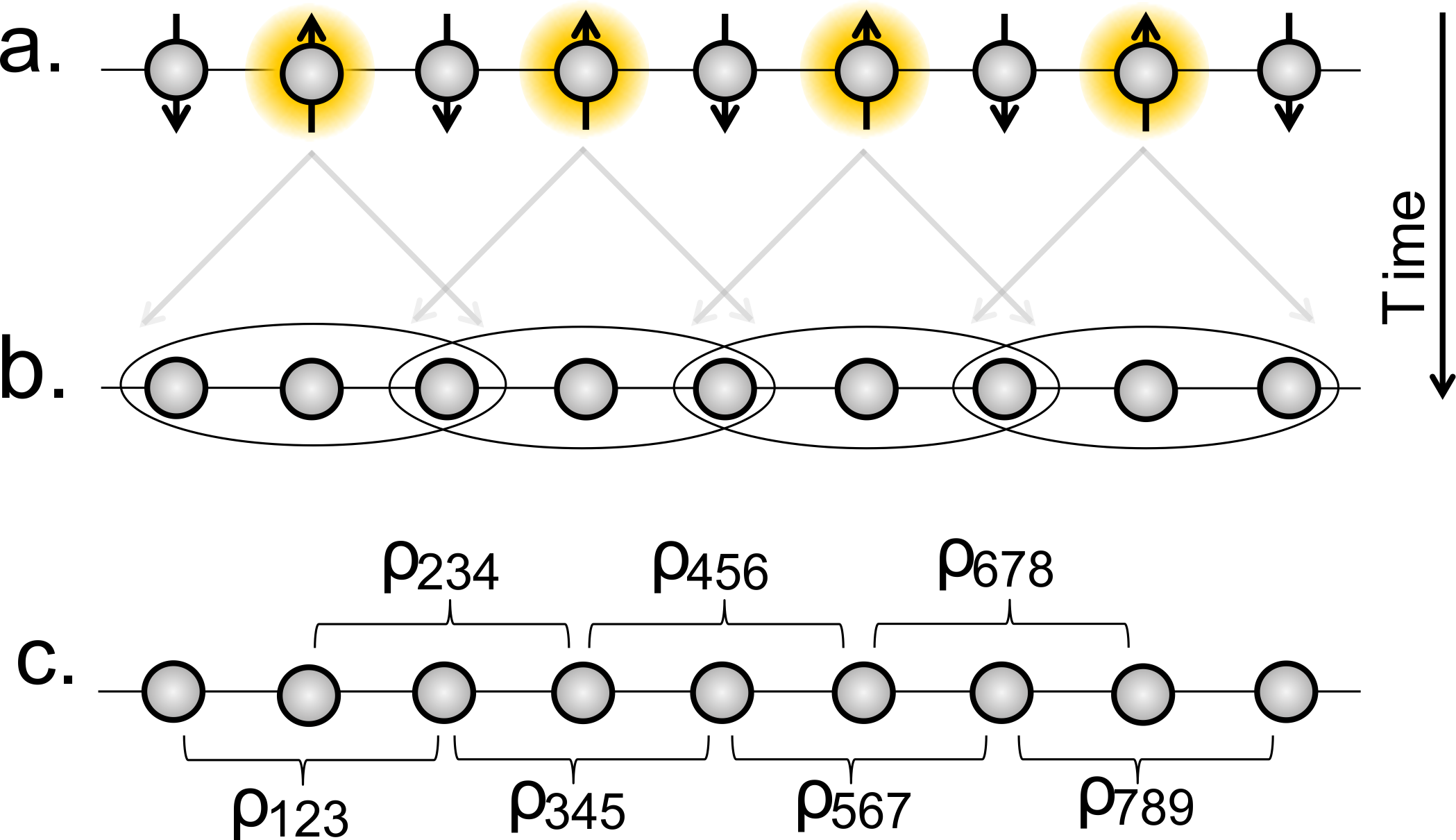
In our trapped-ion simulator, the state of a spin-1/2 particle is encoded in a superposition of two long-lived electronic states of an ion. Spin-spin interactions that fall of with distance are realized by suitably tailored laser pulses that create state-dependent forces acting on the ions. Initially, a string of N ions is prepared in an unentangled product state.  When the interactions are abruptly switched on, quantum correlations start to spread out in the system and begin to entangle larger and larger groups of neighbouring ions.

Our technique for reconstructing the quantum state of the complete system is based on measuring all the correlation functions between groups of ions at distances that are shorter than the maximum distance over which quantum correlations have spread out. These measurements are then fed into a reconstruction algorithm that searches among all MPS states the one that optimally reproduces these correlations. In a second step, additional measurements can be used to obtain lower bound on the fidelity of the experimental state with the reconstructed state, thus resulting in a certified minimum fidelity. Our results reveal the dynamical growth of entanglement and describe its complexity as correlations spread out during a quench which is a necessary condition for future demonstrations of better-than-classical performance.

Literature

[1] H. Häffner et al., Scalable multiparticle entanglement of trapped ions, Nature 438, 643 (2005)
[2] M. Cramer et al., Efficient quantum state tomography. Nat. Commun. 1, 149 (2010).
[3] D. Gross et al., Quantum state tomography via compressed sensing. Phys. Rev. Lett. 105, 150401 (2010).
[4] G. Tóth et al., Permutationally invariant quantum tomography. Phys. Rev. Lett. 105, 250403 (2010).
[5] S. T. Flammia, Y.-K. Liu, Direct fidelity estimation from few Pauli measurements. Phys. Rev. Lett. 106, 230501 (2011).
[6] T. Baumgratz et al., Scalable reconstruction of density matrices. Phys. Rev. Lett. 111, 020401 (2013).
[7] M. Cramer et al., Spatial entanglement of bosons in optical lattices. Nature Commun. 4, 2161 (2013).

Financial support

The work was financially supported by, among others, the Austrian Science Fund FWF and the European Union.

CR, September 2017